Electromagnetic Wave Propagation Animation

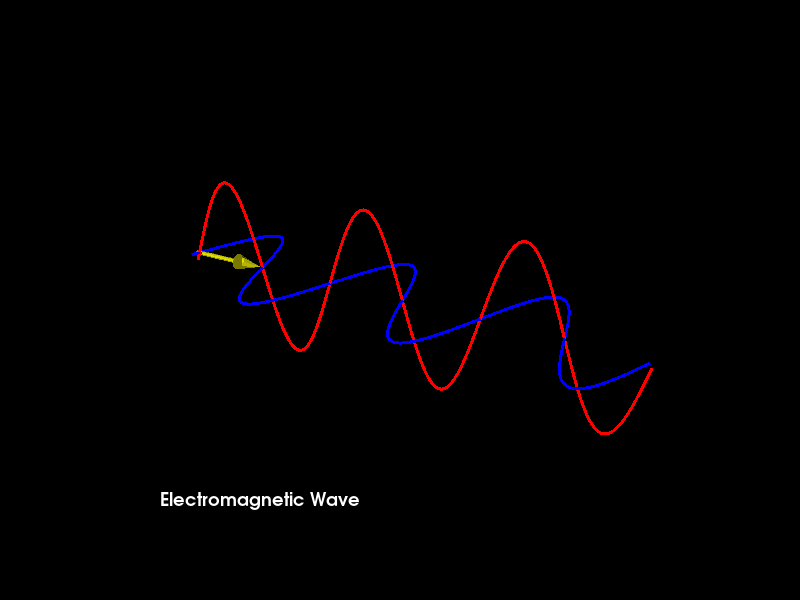
A linearly polarized sinusoidal electromagnetic wave, propagating in the direction +x through a homogeneous, isotropic, dissipationless medium, such as vacuum. The electric field (blue arrows) oscillates in the ±z-direction, and the orthogonal magnetic field (red arrows) oscillates in phase with the electric field, but in the ±y-direction.

Function of the sinusoid used in the animation = sin(k*x - w*t + d) Where, k:wavenumber, x:abscissa, w:angular frequency, t:time, d:phase angle

Importing necessary modules

import itertools

import numpy as np

import fury

function that updates and returns the coordinates of the waves which are changing with time

def update_coordinates(wavenumber, ang_frq, time, phase_angle):
    x = np.linspace(-3, 3, npoints)
    y = np.sin(wavenumber * x - ang_frq * time + phase_angle)
    z = np.array([0 for i in range(npoints)])
    return x, y, z

Variable(s) and their description

npoints: int

For high quality rendering, keep the number of npoints high but kindly note that higher values for npoints will slow down the rendering process (default = 800)

wavelength: int

wavelength of the wave (default = 2)

wavenumber: float

2*pi/wavelength

time: float

time (default time i.e. time at beginning of the animation = 0)

incre_time: float

value by which time is incremented for each call of timer_callback (default = 0.1)

angular_frq: float

angular frequency (default = 0.1)

phase_angle: float

phase angle (default = 0.002)

npoints = 800
wavelength = 2
wavenumber = 2 * np.pi / wavelength
time = 0
incre_time = 0.1
angular_frq = 0.1
phase_angle = 0.002

Creating a scene object and configuring the camera’s position

scene = fury.window.Scene()
scene.set_camera(
    position=(-6, 5, -10), focal_point=(0.0, 0.0, 0.0), view_up=(0.0, 0.0, 0.0)
)
showm = fury.window.ShowManager(
    scene=scene, size=(800, 600), reset_camera=True, order_transparent=True
)

Creating a yellow colored arrow to show the direction of propagation of electromagnetic wave

centers = np.array([[3, 0, 0]])
directions = np.array([[-1, 0, 0]])
heights = np.array([6.4])
arrow_actor = fury.actor.arrow(
    centers,
    directions,
    fury.window.colors.yellow,
    heights=heights,
    resolution=20,
    tip_length=0.06,
    tip_radius=0.012,
    shaft_radius=0.005,
)
scene.add(arrow_actor)

Creating point actor that renders the magnetic field

x = np.linspace(-3, 3, npoints)
y = np.sin(wavenumber * x - angular_frq * time + phase_angle)
z = np.array([0 for i in range(npoints)])

pts = np.array(list(zip(x, y, z)))
pts = [pts]
colors = fury.window.colors.red
wave_actor1 = fury.actor.line(pts, colors=colors, linewidth=3)
scene.add(wave_actor1)

vertices = fury.utils.vertices_from_actor(wave_actor1)
vcolors = fury.utils.colors_from_actor(wave_actor1, array_name="colors")
no_vertices_per_point = len(vertices) / npoints
initial_vertices = vertices.copy() - np.repeat(pts, no_vertices_per_point, axis=0)

Creating point actor that renders the electric field

xx = np.linspace(-3, 3, npoints)
yy = np.array([0 for i in range(npoints)])
zz = np.sin(wavenumber * xx - angular_frq * time + phase_angle)

pts2 = np.array(list(zip(xx, yy, zz)))
pts2 = [pts2]
colors2 = fury.window.colors.blue
wave_actor2 = fury.actor.line(pts2, colors=colors2, linewidth=3)
scene.add(wave_actor2)

vertices2 = fury.utils.vertices_from_actor(wave_actor2)
vcolors2 = fury.utils.colors_from_actor(wave_actor2, array_name="colors")
no_vertices_per_point2 = len(vertices2) / npoints
initial_vertices2 = vertices2.copy() - np.repeat(pts2, no_vertices_per_point2, axis=0)

Initializing text box to display the title of the animation

tb = fury.ui.TextBlock2D(bold=True, position=(160, 90))
tb.message = "Electromagnetic Wave"
scene.add(tb)

end is used to decide when to end the animation

end = 300

Initializing counter

counter = itertools.count()

Coordinates to be plotted are changed every time timer_callback is called by using the update_coordinates function. The wave is rendered here.

def timer_callback(_obj, _event):
    global pts, pts2, time, time_incre, angular_frq, phase_angle, wavenumber
    time += incre_time
    cnt = next(counter)

    x, y, z = update_coordinates(wavenumber, angular_frq, phase_angle, time)
    pts = np.array(list(zip(x, y, z)))
    vertices[:] = initial_vertices + np.repeat(pts, no_vertices_per_point, axis=0)
    fury.utils.update_actor(wave_actor1)

    xx, zz, yy = update_coordinates(wavenumber, angular_frq, phase_angle, time)
    pts2 = np.array(list(zip(xx, yy, zz)))
    vertices2[:] = initial_vertices2 + np.repeat(pts2, no_vertices_per_point2, axis=0)
    fury.utils.update_actor(wave_actor2)

    showm.render()

    # to end the animation
    if cnt == end:
        showm.exit()

Run every 25 milliseconds

showm.add_timer_callback(True, 25, timer_callback)

interactive = False
if interactive:
    showm.start()
fury.window.record(scene=showm.scene, size=(800, 600), out_path="viz_emwave.png")