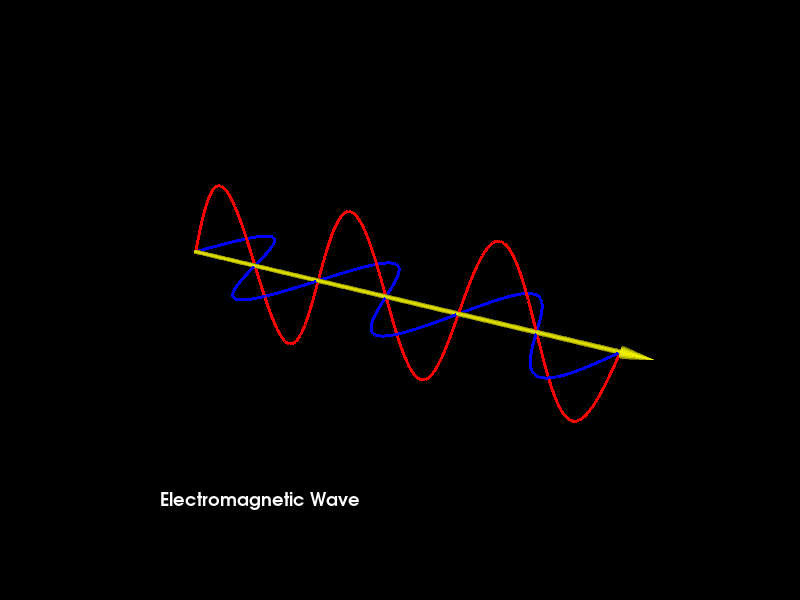
Electromagnetic Wave Propagation Animation

A linearly polarized sinusoidal electromagnetic wave, propagating in the direction +x through a homogeneous, isotropic, dissipationless medium, such as vacuum. The electric field (blue arrows) oscillates in the ±z-direction, and the orthogonal magnetic field (red arrows) oscillates in phase with the electric field, but in the ±y-direction.

Function of the sinusoid used in the animation = sin(k*x - w*t + d) Where, k:wavenumber, x:abscissa, w:angular frequency, t:time, d:phase angle

Importing necessary modules

from fury import window, actor, utils, ui
import numpy as np
import itertools

function that updates and returns the coordinates of the waves which are changing with time

def update_coordinates(wavenumber, ang_frq, time, phase_angle):
    x = np.linspace(-3, 3, npoints)
    y = np.sin(wavenumber*x - ang_frq*time + phase_angle)
    z = np.array([0 for i in range(npoints)])
    return x, y, z

Variable(s) and their description- npoints: For high quality rendering, keep the number of npoints high

but kindly note that higher values for npoints will slow down the rendering process (default = 800)

wavelength : wavelength of the wave (default = 2) wavenumber : 2*pi/wavelength time: time (default time i.e. time at beginning of the animation = 0) incre_time: value by which time is incremented for each call of

timer_callback (default = 0.1)

angular_frq: angular frequency (default = 0.1) phase_angle: phase angle (default = 0.002)

npoints = 800
wavelength = 2
wavenumber = 2*np.pi/wavelength
time = 0
incre_time = 0.1
angular_frq = 0.1
phase_angle = 0.002

Creating a scene object and configuring the camera’s position

scene = window.Scene()
scene.set_camera(position=(-6, 5, -10), focal_point=(0.0, 0.0, 0.0),
                 view_up=(0.0, 0.0, 0.0))
showm = window.ShowManager(scene,
                           size=(800, 600), reset_camera=True,
                           order_transparent=True)
showm.initialize()

Creating a yellow colored arrow to show the direction of propagation of electromagnetic wave

centers = np.array([[3, 0, 0]])
directions = np.array([[-1, 0, 0]])
heights = np.array([6.4])
arrow_actor = actor.arrow(centers, directions, window.colors.yellow, heights,
                          resolution=20, tip_length=0.06, tip_radius=0.012,
                          shaft_radius=0.005)
scene.add(arrow_actor)

Creating point actor that renders the magnetic field

x = np.linspace(-3, 3, npoints)
y = np.sin(wavenumber*x - angular_frq*time + phase_angle)
z = np.array([0 for i in range(npoints)])

pts = np.array([(a, b, c) for (a, b, c) in zip(x, y, z)])
pts = [pts]
colors = window.colors.red
wave_actor1 = actor.line(pts, colors, linewidth=3)
scene.add(wave_actor1)

vertices = utils.vertices_from_actor(wave_actor1)
vcolors = utils.colors_from_actor(wave_actor1, 'colors')
no_vertices_per_point = len(vertices)/npoints
initial_vertices = vertices.copy() - \
    np.repeat(pts, no_vertices_per_point, axis=0)

Creating point actor that renders the electric field

xx = np.linspace(-3, 3, npoints)
yy = np.array([0 for i in range(npoints)])
zz = np.sin(wavenumber*xx - angular_frq*time + phase_angle)

pts2 = np.array([(a, b, c) for (a, b, c) in zip(xx, yy, zz)])
pts2 = [pts2]
colors2 = window.colors.blue
wave_actor2 = actor.line(pts2, colors2, linewidth=3)
scene.add(wave_actor2)

vertices2 = utils.vertices_from_actor(wave_actor2)
vcolors2 = utils.colors_from_actor(wave_actor2, 'colors')
no_vertices_per_point2 = len(vertices2)/npoints
initial_vertices2 = vertices2.copy() - \
    np.repeat(pts2, no_vertices_per_point2, axis=0)

Initializing text box to display the title of the animation

tb = ui.TextBlock2D(bold=True, position=(160, 90))
tb.message = "Electromagnetic Wave"
scene.add(tb)

end is used to decide when to end the animation

end = 300

Initializing counter

counter = itertools.count()

Coordinates to be plotted are changed everytime timer_callback is called by using the update_coordinates function. The wave is rendered here.

def timer_callback(_obj, _event):
    global pts, pts2, time, time_incre, angular_frq, phase_angle, wavenumber
    time += incre_time
    cnt = next(counter)

    x, y, z = update_coordinates(wavenumber, angular_frq, phase_angle, time)
    pts = np.array([(a, b, c) for (a, b, c) in zip(x, y, z)])
    vertices[:] = initial_vertices + \
        np.repeat(pts, no_vertices_per_point, axis=0)
    utils.update_actor(wave_actor1)

    xx, zz, yy = update_coordinates(wavenumber, angular_frq, phase_angle, time)
    pts2 = np.array([(a, b, c) for (a, b, c) in zip(xx, yy, zz)])
    vertices2[:] = initial_vertices2 + \
        np.repeat(pts2, no_vertices_per_point2, axis=0)
    utils.update_actor(wave_actor2)

    showm.render()

    # to end the animation
    if cnt == end:
        showm.exit()

Run every 25 milliseconds

showm.add_timer_callback(True, 25, timer_callback)

interactive = False
if interactive:
    showm.start()
window.record(showm.scene, size=(800, 600), out_path="viz_emwave.png")